FastICA算法原理详解

FastICA算法是一种独立成分分析（ICA）的快速算法，其原理基于非高斯性最大化的目标函数，通过固定点迭代的方式寻找独立成分。FastICA算法能够有效地从多变量数据中提取出非高斯、非线性的独立源信号，具有计算效率高、鲁棒性强的特点，在信号处理、图像处理、生物医学等领域有广泛应用。

FastICA是一种用于独立成分分析（Independent Component Analysis，ICA）的算法，ICA是一种计算方法，用于将多变量信号分离成其独立源的线性组合，FastICA算法以其高效性和稳定性在许多领域得到了广泛应用，特别是在信号处理和数据分析中，本文将详细介绍FastICA算法的原理及其工作方式。

FastICA算法的基本原理

FastICA算法基于非高斯性最大化的原则进行独立成分分析，其基本思想是通过寻找一种线性变换，将观测信号分解为若干个独立成分的线性组合，这些独立成分在统计上是相互独立的，且具有非高斯性。

FastICA算法的核心在于寻找一种使得非高斯性最大的线性变换，非高斯性是一种衡量独立成分的重要指标，因为独立成分往往具有非高斯分布的特性，FastICA算法通过最大化非高斯性，从而有效地提取出观测信号中的独立成分。

FastICA算法的步骤

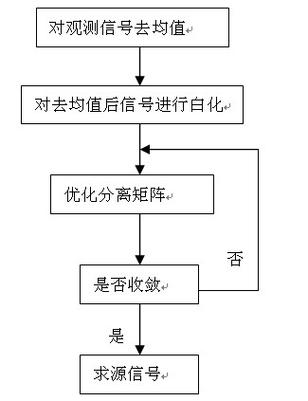
1、数据预处理：对观测信号进行中心化处理，使其均值为零，这一步是为了消除数据中的直流分量，使得算法更加稳定。

2、初始化权重向量：随机生成一组权重向量，作为算法的初始值。

3、计算独立成分：利用FastICA算法的核心思想，通过迭代计算，逐步更新权重向量，从而得到观测信号的独立成分。

4、迭代更新：在每一次迭代中，计算当前权重向量下的非高斯性，并根据非高斯性的大小调整权重向量，使得非高斯性最大化。

5、收敛判断：当算法达到预设的迭代次数或非高斯性不再显著提高时，算法停止迭代，输出独立成分。

FastICA算法的优点

1、高效性：FastICA算法采用迭代的方式逐步更新权重向量，从而提取出观测信号中的独立成分，其计算复杂度较低，具有较高的计算效率。

2、稳定性好：FastICA算法对初始值的选择不敏感，具有较强的鲁棒性，该算法在处理具有非高斯分布的观测信号时，能够有效地提取出独立成分。

3、可解释性强：FastICA算法提取出的独立成分具有明确的物理意义，便于后续的数据分析和解释。

FastICA算法的应用

FastICA算法在许多领域得到了广泛应用，在信号处理领域，FastICA算法可以用于语音增强、图像去噪、脑电信号分析等，在数据分析领域，FastICA算法可以用于特征提取、数据降维、图像识别等任务，FastICA算法还可以与其他机器学习算法相结合，进一步提高模型的性能和鲁棒性。

本文详细介绍了FastICA算法的原理及其工作方式，FastICA算法是一种基于非高斯性最大化的独立成分分析算法，具有高效性、稳定性和可解释性强等优点，该算法在信号处理和数据分析等领域得到了广泛应用，为解决实际问题提供了有效的工具，随着机器学习和人工智能技术的不断发展，FastICA算法将在更多领域得到应用和优化。

展望

尽管FastICA算法已经取得了显著的成果，但仍有许多潜在的研究方向和改进空间，可以进一步研究FastICA算法的理论基础，提高其数学严谨性和可解释性，可以探索将FastICA算法与其他机器学习算法相结合，以提高模型的性能和鲁棒性，还可以将FastICA算法应用于更多领域，如生物医学、金融分析等，以解决实际问题并推动相关领域的发展。

FastICA算法作为一种有效的独立成分分析方法，在信号处理和数据分析等领域具有广泛的应用前景，随着机器学习和人工智能技术的不断发展，FastICA算法将发挥更大的作用，为解决实际问题提供更多有效的工具和手段。